なんでストロボのGNはストロボから被写体までの距離なのか

普段からPhoto Cafeteriaさんの動画を楽しく視聴させていただいています。
この動画ではSony a9IIIはグローバルシャッターなのでちっちゃなストロボで十分だよ!ということが言われているのですが、そのなかでストロボのガイドナンバーGNの計算がよくわかりませんでした。
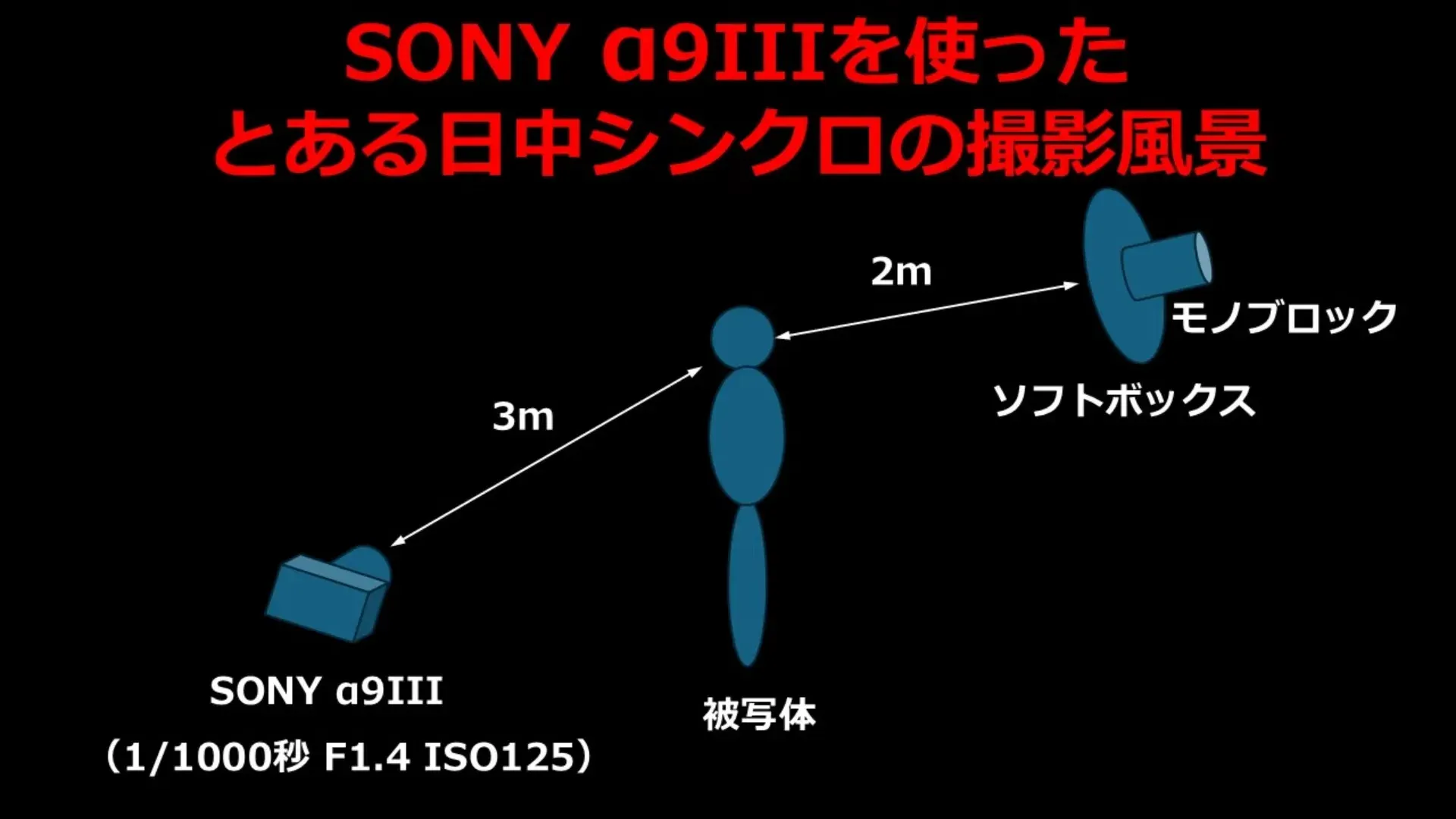
動画の図を見ると、ストロボから被写体まで2m、カメラから被写体まで3mという配置になっています。で、GNの計算に使われているのは2mの方なんですよね。
式:ガイドナンバー(GN)=距離(m)×絞り値(F値)

てっきり\(\text{GN} = 3 \times 1.4 = 4.2\)かなと思ったのですが、正しくは\(\text{GN} = 2 \times 1.4 = 2.8\)だそうです。
普段はオフカメラライティングをしたことがないので、なんでだろうなあと。
「別の機会にお話しする」と言っていましたが、気になって仕方ないので自分であれこれ考えてみました。
端的な解説
答え:被写体を照らすのはストロボだから
GNの計算で使う距離は、常に「光源から被写体までの距離」です。
理由
- 光の逆二乗の法則:ストロボから2m離れた被写体の明るさは、ストロボの光量と2mという距離で決まる
- 被写体は光を反射するだけ:被写体は拡散反射面として、受けた光を周囲に散らす。どの角度から見ても同じ明るさ
- カメラは傍観者:カメラはすでに照らされた被写体を見るだけ。カメラの位置は被写体の明るさに影響しない
オンカメラとの違い
- オンカメラ:ストロボ=カメラの位置なので、結果的に「カメラから被写体までの距離」を使う
- オフカメラ:ストロボとカメラが別の場所にあるので、「ストロボから被写体までの距離」を使う
つまり、常に光源からの距離で考えれば迷いません。
ストロボのガイドナンバー(GN)を物理的に理解する
今回は、その理由を数式と物理の基礎から丁寧に追っていきましょう。
次元とは何か?
数式を扱う前に、「次元」という概念を理解しておきましょう。次元とは、物理量が持つ「種類」のようなものです。
たとえば:
- 距離は「長さ」の次元を持ちます。メートル(m)で測ります。
- 時間は「時間」の次元を持ちます。秒(s)で測ります。
- 速度は「長さ÷時間」の次元を持ちます。m/sで測ります。
なぜこれが大事かというと、物理的に意味のある式では、等号の両辺の次元が必ず一致するからです。これを「次元の整合性」と呼びます。
例えば、「距離 = 速度 × 時間」という式を考えてみましょう。
- 左辺:距離の次元は \([\text{長さ}] = [L]\)
- 右辺:速度 × 時間の次元は \([L/T] \times [T] = [L]\)
両辺の次元が \([L]\) で一致していますね。もし一致していなければ、その式は物理的に間違っているということです。
これから導出するGNの式 \(\text{GN} = F \times d\) についても、次元を追いかけることで、「なぜこの式が成り立つのか」「各項が何を意味するのか」が明確になります。
登場する物理量を整理する
写真の露出に関わる物理量を、1つずつ定義していきましょう。ここでは次元を以下のように表記します:
- \([L]\) :長さ(Length)
- \([T]\) :時間(Time)
- \([M]\) :質量(Mass)- エネルギーの次元で使います
ストロボが発する光のエネルギー
ストロボが発光したとき、総エネルギー \(P\) が放出されます。これは「ストロボの光量」とも呼ばれ、一般にジュール(J)で測られます。エネルギーの次元は:
\[ [P] = \text{エネルギー} = [ML^2T^{-2}] \]
この式は、エネルギー = 質量 × 速度の2乗から来ています。
運動エネルギーの式から次元を追っていきましょう。
\[ E = \frac{1}{2}mv^2 \]
- 質量 \(m\) の次元: \([M]\)
- 速度 \(v\) の次元: \([L/T] = [LT^{-1}]\) (距離÷時間)
- 速度の2乗 \(v^2\) の次元: \([LT^{-1}]^2 = [L^2T^{-2}]\)
したがって、運動エネルギー \(E = mv^2\) (定数の1/2は次元に影響しないので省略)の次元は:
\[ [E] = [M] \times [L^2T^{-2}] = [ML^2T^{-2}] \]
つまり:
- 質量 \([M]\) が1つ
- 長さ \([L]\) が2乗
- 時間 \([T]\) が-2乗(つまり分母に時間の2乗)
この次元は運動エネルギーだけでなく、位置エネルギー( \(mgh\) )や熱エネルギー、光のエネルギーなど、すべてのエネルギーに共通する次元です。
照度:ある場所での光の強さ
ストロボから距離 \(d\) [m] 離れた場所での「光の強さ」を考えます。これを照度(Illuminance)と呼び、記号 \(I\) で表します。照度は「単位面積あたりに届く光のエネルギー」なので、その次元は:
\[ [I] = \frac{\text{エネルギー}}{\text{面積}} = \frac{[ML^2T^{-2}]}{[L^2]} = [MT^{-2}] \]
実際の単位はルクス(lx)などですが、ここでは本質的な次元に注目します。
F値:レンズの絞り
カメラのレンズには「絞り」があり、これがどれだけ光を通すかを決めます。F値は「焦点距離 ÷ 有効開口径」として定義されます:
\[ F = \frac{\text{焦点距離}}{\text{有効開口径}} = \frac{[L]}{[L]} = \text{無次元} \]
F値自体は無次元の数値です(F2.8、F4、F5.6など)。数字が小さいほど、たくさんの光が入ります。
しかし、実際に重要なのはレンズの開口面積 \(A\) です。レンズを正面から見たときの「光が通る穴の面積」です。この面積は、F値の2乗に反比例します:
\[ A \propto \frac{1}{F^2} \]
開口面積の次元は明らかに:
\[ [A] = [L^2] \]
露光量:センサーに届く光のエネルギー
最終的にカメラのセンサーに届く光のエネルギーを露光量(Exposure)と呼び、記号 \(E\) で表します。これも次元はエネルギーなので:
\[ [E] = [ML^2T^{-2}] \]
写真が「明るく写る」か「暗く写る」かは、この露光量で決まります。
光の広がり方:逆二乗の法則
ストロボは小さな点から光を放出すると考えます(点光源の近似)。この光は球面状に、全方向に均等に広がっていきます。
距離 \(d\) の位置で、光はどのくらい広がっているでしょうか?光が作る球面の表面積は:
\[ S = 4\pi d^2 \quad [L^2] \]
ストロボの総エネルギー \(P\) は、この球面全体に分散されます。したがって、単位面積あたりに届くエネルギー、つまり照度 \(I\) は:
\[ I(d) = \frac{P}{4\pi d^2} \]
次元を確認してみましょう:
\[ [I] = \frac{[P]}{[d^2]} = \frac{[ML^2T^{-2}]}{[L^2]} = [MT^{-2}] \]
照度の次元として正しいですね!
この式から、距離が2倍になると照度は1/4になることがわかります:
\[ I(2d) = \frac{P}{4\pi (2d)^2} = \frac{P}{4\pi \cdot 4d^2} = \frac{1}{4} \cdot \frac{P}{4\pi d^2} = \frac{I(d)}{4} \]
これが有名な光の逆二乗の法則です。
被写体の役割:光を反射する面
ここで重要な考え方をします。ストロボの光は直接カメラに届くのではなく、被写体に当たって反射した光がカメラに届きます。
被写体は、ストロボの光を受けて、それを周囲に反射します。ここで、被写体が拡散反射面(ランベルト面)であると仮定します。これは、光沢のある鏡のような表面ではなく、紙や布、人の肌のような、マットな表面です。
拡散反射面の特徴は、どの方向から見ても同じ明るさに見えることです。つまり、被写体からの反射光の輝度(明るさ)は、照度 \(I\) に比例し、見る角度によらず一定です。これが、オフカメラライティングでカメラの位置がある程度自由である理由です。
数式で書くと、被写体の輝度(Luminance)を \(L_{\text{subject}}\) とすると:
\[ L_{\text{subject}} \propto I \]
被写体が明るく照らされているほど( \(I\) が大きいほど)、被写体は明るく見えます。
カメラに届く光量の計算
さて、被写体から反射された光のうち、どれだけがカメラのセンサーに届くでしょうか?
カメラのレンズは、被写体からの光を集めます。レンズが集める光の量は、次の2つの要素で決まります:
- 被写体の輝度 \(L_{\text{subject}}\) :被写体が明るいほど、たくさんの光が反射される
- レンズの開口面積 \(A\) :開口が大きいほど、たくさんの光を集められる
したがって、センサーに届く露光量 \(E\) は:
\[ E \propto L_{\text{subject}} \times A \]
被写体の輝度は照度に比例する( \(L_{\text{subject}} \propto I\) )ので:
\[ E \propto I \times A \]
さらに、 \(I = P/(4\pi d^2)\) と \(A \propto 1/F^2\) を代入すると:
\[ E \propto \frac{P}{4\pi d^2} \times \frac{1}{F^2} = \frac{P}{4\pi d^2 F^2} \]
比例定数をまとめて \(k\) とすると:
\[ E = k \cdot \frac{P}{d^2 F^2} \]
次元を確認しましょう:
\[ [E] = \frac{[P]}{[d^2][F^2]} = \frac{[ML^2T^{-2}]}{[L^2] \cdot [1]} = [ML^2T^{-2}] \]
露光量の次元として正しいです!
適正露出の条件:ガイドナンバーの導出
写真が適正露出(ちょうど良い明るさ)になるためには、露光量 \(E\) が特定の値 \(E_0\) になる必要があります。この \(E_0\) は、ISO感度の設定によって決まります。ISO感度を上げると、より少ない光量(小さい \(E_0\) )で適正露出になります。
適正露出の条件は:
\[ E = E_0 \]
つまり:
\[ k \cdot \frac{P}{d^2 F^2} = E_0 \]
この式を整理すると:
\[ d^2 F^2 = k \cdot \frac{P}{E_0} \]
右辺は、ストロボの出力 \(P\) とISO感度( \(E_0\) に反映)だけで決まる定数です。この定数を \(\text{GN}^2\) と定義します:
\[ d^2 F^2 = \text{GN}^2 \]
両辺の平方根を取ると:
\[ d \cdot F = \text{GN} \]
これがガイドナンバーの式です!
次元を確認すると:
\[ [\text{GN}] = [d \cdot F] = [L] \cdot [1] = [L] \]
GNは長さの次元を持ち、実際にメートル(m)で表されます。
なぜ単純な反比例になるのか?
光の強さは距離の2乗に反比例するのに( \(I \propto 1/d^2\) )、なぜGNの式では \(F \propto 1/d\) という単純な1乗の反比例になっているのでしょう?
けっこう不思議に思いませんか?
答えは、逆二乗の効果が2回現れるからです。
露光量 \(E\) の式をもう一度見てみましょう:
\[ E \propto \frac{1}{d^2} \times \frac{1}{F^2} \]
- 第1の逆二乗:光の強さが距離の逆二乗 \(d^{-2}\) に比例
- 第2の逆二乗:レンズの開口面積がF値の逆二乗 \(F^{-2}\) に比例
この2つの逆二乗を掛け合わせると:
\[ E \propto d^{-2} \times F^{-2} = (d \times F)^{-2} \]
適正露出では \(E = E_0 =\) 一定なので:
\[ (d \times F)^{-2} = \text{一定} \]
したがって:
\[ d \times F = \text{一定} = \text{GN} \]
逆二乗が2つ掛かることで、平方根を取ったときに1乗の関係になるのです。これがGNの式の数学的な本質です。
具体例で実感する
理論だけだとピンとこないかもしれないので、具体的な数値で追ってみましょう。
初期状態:
- ストロボから被写体まで: \(d = 2\) m
- F値: \(F = 2.8\)
- 照度: \(I = P/(4\pi d^2) = P/(4\pi \cdot 4) = P/(16\pi)\)
距離を2倍にした状態(4mに):
- 距離: \(d' = 4\) m
- 照度: \(I' = P/(4\pi \cdot 16) = P/(64\pi) = I/4\)
照度が1/4になりました。これだけだと、写真は暗くなってしまいます。
F値を調整して露出を保つには?
GNの式 \(d \times F = \text{GN}\) より:
\[ F' = \frac{\text{GN}}{d'} = \frac{2.8 \times 2}{4} = \frac{5.6}{4} = 1.4 \]
F値を2.8から1.4に変更(2段開ける)します。
F値が半分になると、開口面積は何倍になるでしょう? \(A \propto 1/F^2\) なので:
\[ \frac{A'}{A} = \frac{F^2}{F'^2} = \frac{(2.8)^2}{(1.4)^2} = \frac{7.84}{1.96} = 4 \]
開口面積が4倍になりました。
露光量の変化:
\[ \frac{E'}{E} = \frac{I'}{I} \times \frac{A'}{A} = \frac{1}{4} \times 4 = 1 \]
照度が1/4になっても、開口面積を4倍にすることで、露光量は変わらず、適正露出が保たれます。これが \(d \times F = \text{一定}\) の物理的な意味です。
オンカメラ vs オフカメラ
さて、ここからが重要です。動画で提示された2つのケースを見てみましょう。
ケース1:オンカメラストロボ
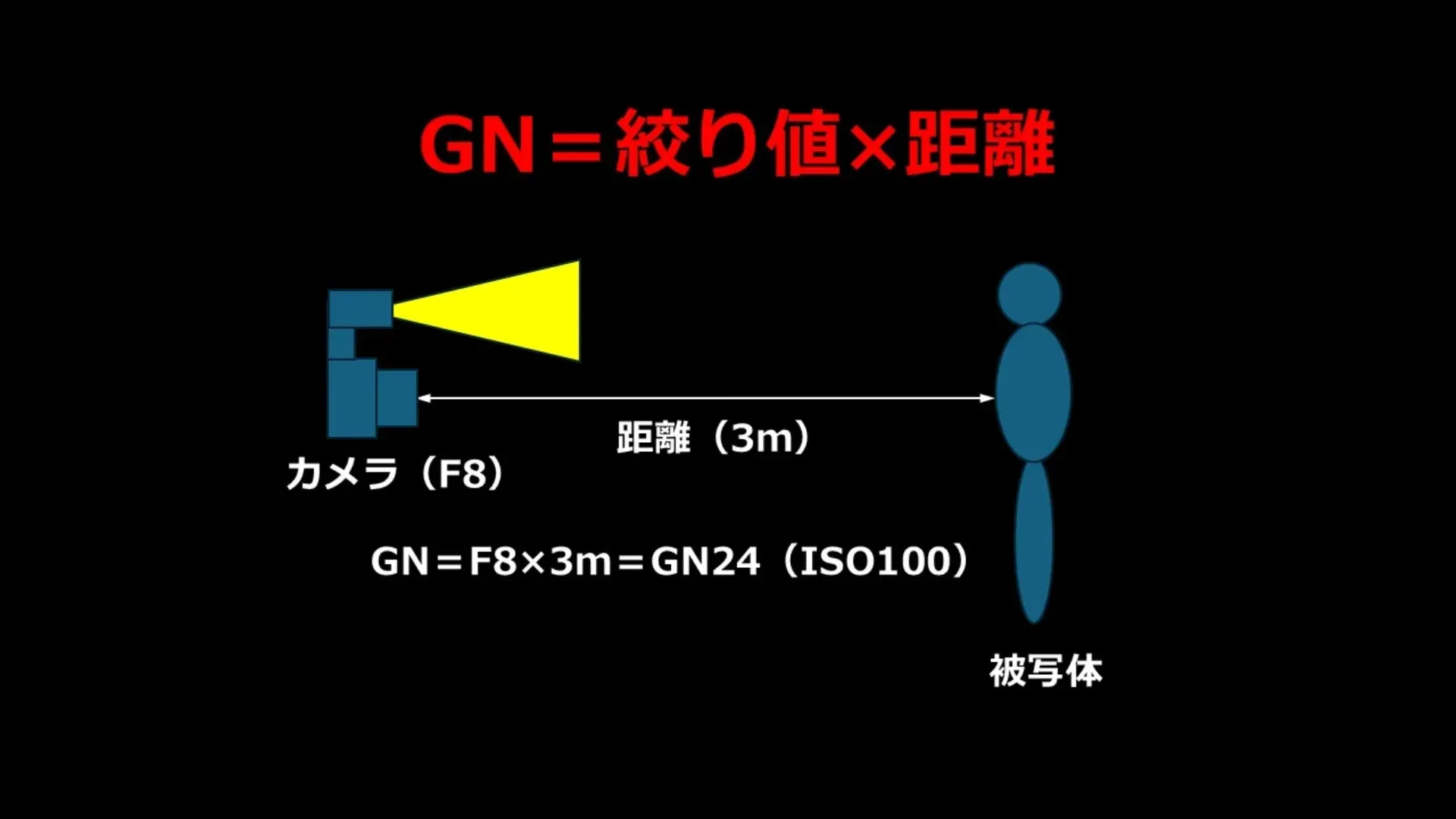
- カメラにストロボが付いている
- カメラ(=ストロボ)から被写体まで:3m
- 設定:F8、ISO 100
この場合、ストロボとカメラは同じ位置にあるので、「カメラから被写体までの距離」=「ストロボから被写体までの距離」です。したがって、GNの計算に使う距離は3mになります。
\[ \text{GN} = F \times d = 8 \times 3 = 24 \]
ISO 100でGN24のストロボが必要、ということですね。
ケース2:オフカメラライティング
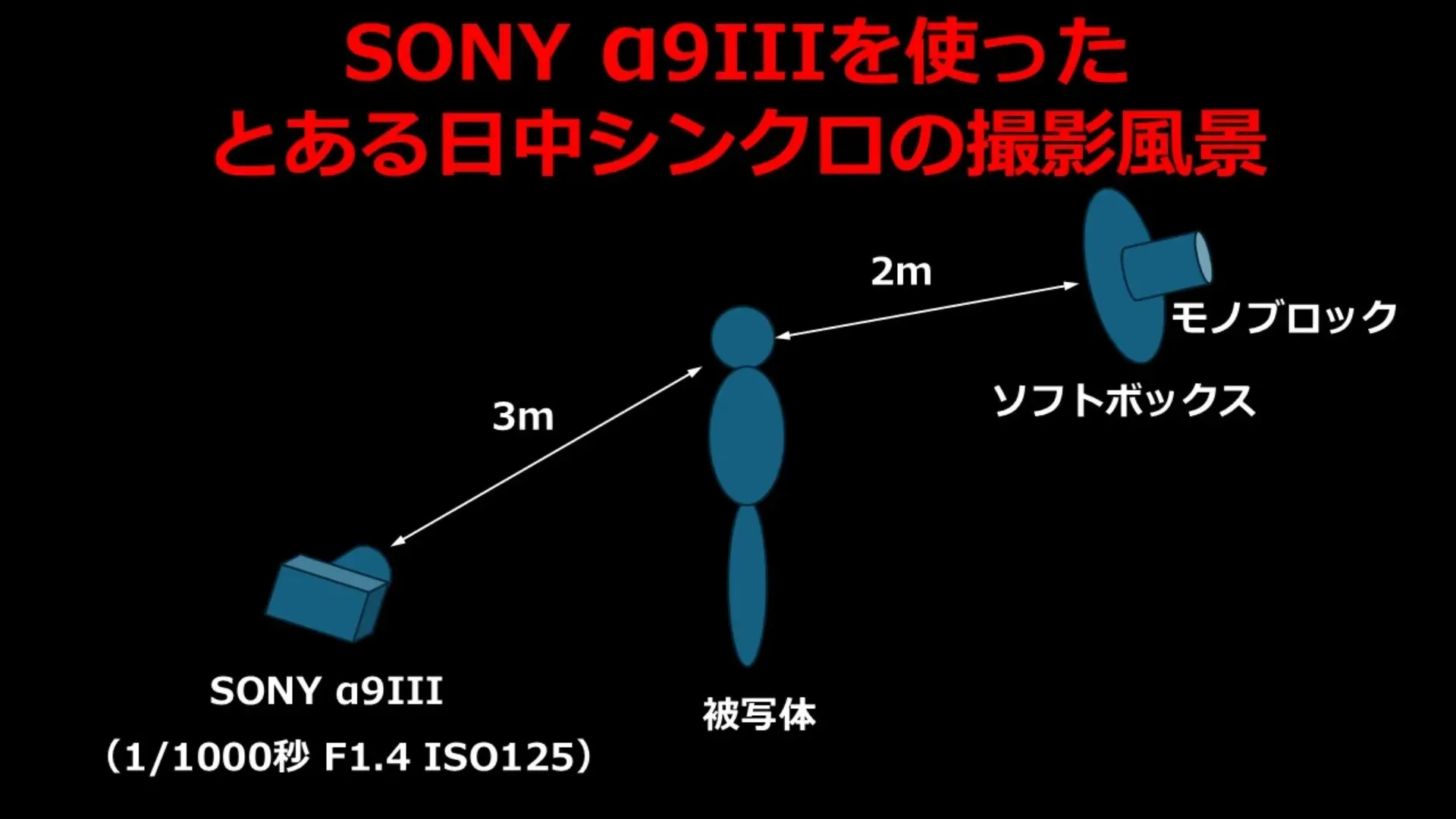
- ストロボから被写体まで:2m
- カメラから被写体まで:3m
- ストロボのGN:2.8(ISO 125)
この場合、GNの計算に使う距離はストロボから被写体までの2mです。なぜなら、被写体の照度を決めるのはストロボからの距離だからです。
\[ F = \frac{\text{GN}}{d} = \frac{2.8}{2} = 1.4 \]
動画の設定(F1.4、1/1000秒、ISO 125)と一致します。
カメラから被写体までの3mは、この計算には直接影響しません。なぜなら、被写体は拡散反射面なので、どこから見ても同じ明るさに見えるからです。(厳密には大気による減衰などの影響がありますが、数メートルの距離では無視できます)
なぜオフカメラでは3m/5mを使わないのか?
オンカメラの場合は「カメラ=ストロボ」なので、カメラまでの距離を使います。しかし、オフカメラの場合、ストロボとカメラは別の位置にあります。
被写体の明るさ(照度)を決めるのは、光源(ストロボ)からの距離です。カメラの位置は、被写体を照らすこととは無関係です。カメラは、すでに照らされた被写体から反射してくる光を受け取るだけです。
だから、オフカメラライティングでは「ストロボから被写体までの距離」を使い、オンカメラストロボでは「カメラ(=ストロボ)から被写体までの距離」を使うのです。
Sony a9IIIとグローバルシャッターの意義
ここまでの理解を踏まえて、動画のポイントを整理しましょう。
従来のカメラのメカニカルシャッターやローリングシャッターでは、フラッシュ同調速度に制限があります(通常1/200〜1/250秒)。これより速いシャッターでストロボを使うと、センサーの一部しか露光されず、画面に黒い帯が出てしまいます。
Sony a9IIIはグローバルシャッターを採用しています。これは、センサー全体が同時に露光される方式で、どんなに高速なシャッター(1/8000秒など)でもストロボと完全に同調します。
これの何が嬉しいのか?
明るい屋外(日中)で撮影するとき、背景を適正露出にするには絞りを絞るか(F値を大きく)、シャッター速度を速くする必要があります。しかし、開放F値(F1.4など)でボケた背景を作りたい場合、シャッター速度を速くするしかありません。
従来のカメラでは、シャッター速度が同調速度に制限されるため、開放F値では背景が明るく飛んでしまいます。ところが、グローバルシャッターなら、1/8000秒のような超高速シャッターを使えるので、開放F値でも背景を暗くできます。
そして、被写体はストロボで照らすので明るく写ります。しかも、オフカメラライティングでストロボを被写体に近づければ、小型のストロボ(GN 2.8程度)で十分な光量が得られるのです。
動画の例では:
- F1.4、1/1000秒 → 背景を暗く(日中でも)
- GN2.8、距離2m → 被写体を明るく
このバランスで、日中でも小型ストロボだけで印象的なポートレートが撮れる、というわけです。
まとめ
GNの式 \(\text{GN} = F \times d\) は、次の物理現象を反映しています:
- 光の逆二乗の法則:距離が遠いほど光は弱くなる( \(\propto 1/d^2\) )
- レンズの光学特性:F値が小さいほど光をたくさん集める( \(\propto 1/F^2\) )
- この2つの逆二乗が組み合わさって、単純な反比例( \(F \propto 1/d\) )になる
これでGNの計算に使う距離は、ストロボから被写体までの距離(被写体を照らすのはストロボだから)なのがよーくわかったと思います。


